Several articles have been devoted in the past to a discussion of the thin film interference phenomenon, which is responsible for the colorful toning we see on silver coins. I would like to delve more deeply into the physics, to see if we can develop a model for understanding and predicting the actual "standard progression" of colors that we observe on silver coins.

For example, why does toning start out light gold? Why does it then progress to gold, amber, russet, burgundy, cobalt blue, light blue, lemon yellow, orange, red, magenta, blue, blue-green, emerald green, and so on. Why can't a coin have gold toning that progresses to green, or some other color, rather than following the "standard progression?"

It turns out that once you understand the thin film interference mechanism, it is possible to model the colors that we actually observe on the coins. As has been shown before, the light reflecting off the surface of a toned coin looks something like this:

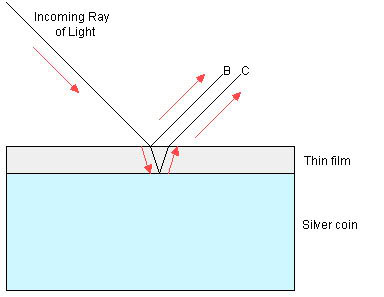
Some of the incoming light reflects off the upper surface of the toning layer, and exits as ray B. However, a portion of the light travels through the thin film layer, and then reflects off the denser metal surface of the coin underneath the toning layer, and exits as ray C. Notice that the light in ray C has to travel a longer distance than ray B. The extra distance (d) traveled is approximately twice the thickness of the toning layer (t). [More accurately, d=2t/sin(x), where x is the angle of incidence of the light hitting the coin's surface below the toning. For light coming in at a direct perpendicular to the surface, x=90°, sin(x)=1, and d=2t.]

Because ray C travels the extra distance, the emerging reflected light of ray C is phase-shifted relative to ray B. If the extra distance traveled by ray C is precisely equal to the wavelength of the light (or a multiple thereof), then the two re-united beams B and C will be in phase, and there will be constructive interference, or reinforcement, of the luminosity at that wavelength. If the extra distance d is precisely equal to one-half the wavelength of the light (or an odd multiple thereof), then the two re-united beams will be precisely out of phase, and there will be destructive interference, or cancellation, of the light at that wavelength. For intermediate phase-shifts, there will be moderate cancellation or reinforcement.

(I am leaving out more details, such as one-half wavelength phase shifts due to differences in the index of refraction of air vs. the toning layer.)

So what we have so far, is that for a given thickness of toning layer, and a given wavelength of light, there will be either constructive interference (reinforcement), or destructive interference (cancellation) of the light as a result of the toning layer. As the toning layer thickness increases, the beams B and C go in and out of phase.

The next step is to understand how we perceive light. Visible light covers a spectrum of wavelengths from about 400 nanometers (nm) for violet to about 700 nm for deepest red. A rainbow occurs when full-spectrum light (i.e. light containing all wavelengths in the visible spectrum) is refracted by a prism, and separated out into all the different wavelengths. For each color in the spectrum, there is a corresponding wavelength of light. However, the way we perceive light is peculiar to the design of our retina, with its "rods" and "cones" (the photoreceptors). The cones perceive color, and there are three types of cones in the human eye. Each one has a peak sensitivity at a particular wavelength:

The three types of cones are B=blue (peak sensitivity at about 440 nm), G=green (535 nm), and R=red (575 nm). The peak sensitivity wavelengths vary in different sources and papers on the subject, but you get the idea.

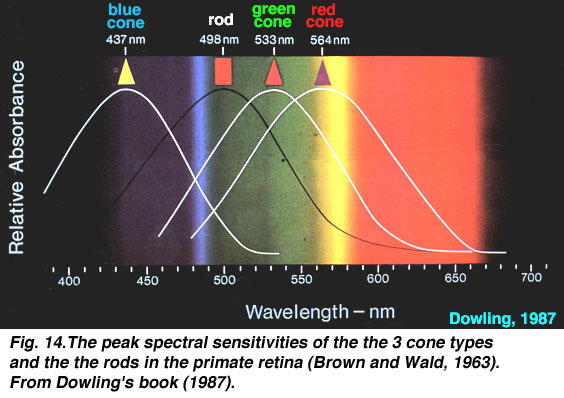
So for example, when our eye sees yellow light, we know it is yellow because of the way our red and green cones respond to it, and our brain translates that into a perception of yellow. The peculiar consequence of our having three specific cone receptors, rather than one that covers the entire spectrum, is that you can "trick" the human eye. If the incoming light contains only two wavelengths - red and green - the eye will perceive it as yellow, just as though the incoming light were at the wavelength for yellow. So I write: G+R=Y. Similarly, blue light plus green light will be perceived as cyan (B+G=C), and blue light plus red light will be perceived as magenta (B+R=M). The combination of all three is perceived as white: B+G+R=W.

Because of this, if you take full-spectrum light, and remove all the blue wavelengths, that means only the red and green cones can respond, and the eye sees yellow. This is called the "subtractive" property of light, which refers not to the light itself, but the way we perceive it. Yellow paint, for example, actually looks yellow because it contains pigments that absorb blue light. We can represent this algebraically as follows: W-B = (B+G+R)-B = G+R = Y

So, if the toning layer has a thickness that results in the cancellation of blue light, then the coin will appear yellow. Depending on which wavelengths get destructively cancelled or constructively reinforced at a particular toning layer thickness, the exit light will have some combination of components of light that appears white (R+G+B), yellow (R+G), cyan (B+G), magenta (B+R), blue (B), green (G), and red (R).

Example: if the incoming light has 4 units each of B, G, R; but the exit light after interference has 3 units B, 2 units G, and 1 unit R, what will we see? We will see a combination of one unit white (B+G+R), one unit cyan (B+G), and one unit blue (B). The result will be a light cyan-blue.

If the exit light contains four units B, five units G, four units R, we will see four units white (B+G+R), plus one leftover units of green. This will give us a bright light green.

If the exit light contains one unit B, five units G, one unit R, we will see one unit white (B+G+R), plus four leftover units of green. This will give us a stronger deeper (less bright) green.

In this way, I can model and predict the color of the exit light. [For the technical among you, the model depends on choosing the right peak wavelengths to represent blue, green and red as seen by our cone photoreceptors. There is some latitude in the numbers chosen, particularly for red; I'm not sure whether the peak sensitivity of 575nm is the right choice, or perhaps a higher number up to 660nm. For our purposes I am assuming the angle of incidence "x" equals 90°, and I am ignoring the half-wavelength shift off the upper surface due to the refractive index change, which actually would imply that light gold toning becomes visible at even lower layer thicknesses.] Here then is a sample spreadsheet:

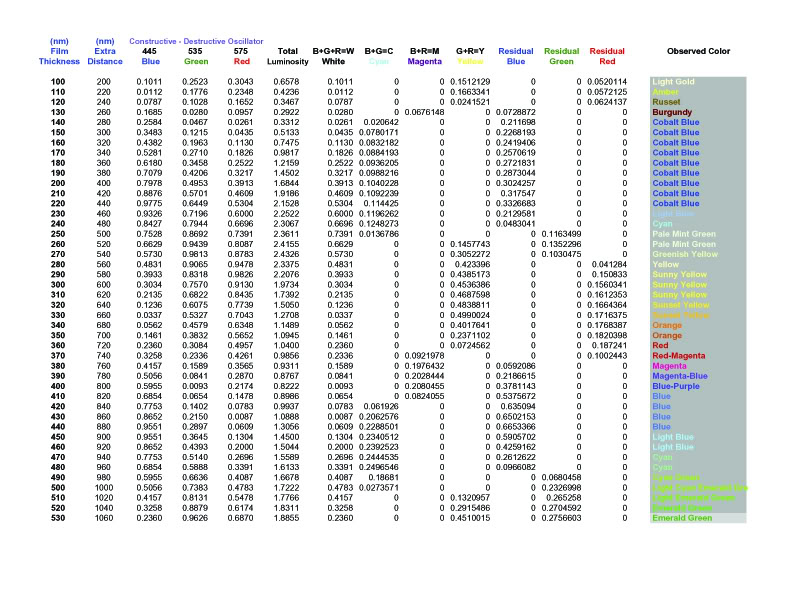
(Click on the picture to view the full size non blurry example - Opens in new window)

It still requires some tweaking, but this approach is on the right track, and basically predicts what we see on the coins. So for example, why does toning start out in the gold-amber category, before we see any blue? Because blue light has the shortest wavelength of the three cones, at 440 nm. That means the phase shift to cancel blue light is about 220 nm, which requires a toning layer of about 110 nm (ignoring the angle x mentioned above). So the very thinnest toning layers cancel blue before they cancel anything else, and when you cancel blue, you are left with R+G=Y, so toning always begins with faint yellow (gold), deepening to amber, russet, and burgundy, before we suddenly get blue, as predicted in the spreadsheet.

This is not quite complete or perfect, but I hope it helps to understand the origin of the magnificent colors we see on toned silver coins, such as this one:

(Photography by Brandon Kelley)

Arguments and Rebuttals:

<<what is this thin film on some silver coins and not others?

is it part of the minting process, or acquired by the coin later?>>

The thin film we are talking about here is a layer of molecular compounds that form naturally at the coin's surface over time. Silver coins are typically struck from an alloy of composition 90% silver - 10% copper. Both silver and copper are somewhat reactive with both oxygen and sulfur. As a result, under natural storage conditions (unless the coin is stored in a vacuum or a completely inert environment such as a helium or argon atmosphere), a layer of "patina" or "toning" will form at the surface of the coin, comprising molecules of silver sulfide, copper oxide, etc.

Anyone who has owned silver or silver-plated housewares will know that eventually they begin to show color over time. Therefore most silver ends up getting dipped or polished periodically to keep it bright and shiny. The same is true of silver coins. There are some exceptions; if a coin is stored in an environment that is non-reactive, it may stay bright over time.

This thin-film layer of toning molecules has a thickness. If the layer forms uniformly over the whole surface of the coin, the color will then appear similarly uniform. In an old-time coin album, for example a Wayte Raymond cardboard coin board, the perimeter of the coin is in contact with the cardboard, which may contain elevated levels of sulfur. As the cardboard outgasses slowly over a period of months and years, the coin acquires toning from the perimeter inward. The result is peripheral or target toning, with the thickest part of the toning layer at the perimeter of the coin. The coin will exhibit a color progression from the center (least toned, thinner toning layer) to the perimeter (most toned, thicker toning layer). The Gobrecht dollar I use as my avatar is an example. The light blue at the extreme perimeter actually represents the thickest toning layer (exactly as predicted by my model) even though it looks lighter in color.

With Morgan dollars, there was a unique opportunity for incredible multi-colored banded rainbow toning to develop. The reason is that, because of politics and history, many many thousands were stored in sealed bank vaults, undisturbed for decades in the original canvas Mint bags (1000 per bag). These storage conditions allowed some of the coins in these bags (the ones at the surface, near to or in contact with the Mint bag fabric) to acquire a thin film toning layer extremely slowly, over a period of many years, due to an almost negligible air flow in the vaults. A toning layer so acquired, extremely slowly, can be quite stable (for reasons of inorganic chemistry more complex than I will tackle here). Due to a very slight diffusion of gases from the outside of the Mint bags to the inside, the toning took the form of a very thin film with gradations in the thickness across the surface of the coin, rather than uniform thickness.

<<Given the explaination above, would the coin you posted (I quoted here) then have a multi-level "thin film) profile if the coin were viewed along the plane of the coins surface? Somewhat of a mountain range profile? Is that what explains the multiple colours or is it all the same depth of film and the colour progression is based on angle of light? >>

It is the gradations of thickness that produce the observed color progression. On the Morgan dollar that I posted above, the thinnest part of the toning layer is at the top of the coin, at the BU of PLURIBUS. The thickest toning layer are the small dark patches between the stars and the rim at 7 o'clock. Viewed in profile, the toning layer would be a slightly inclined plane, rather than a mountain range with ups and downs. Rotating the coin in light shifts the perceived colors only slightly; the angle of incoming light seems to have less of an effect than the thickness of the toning layer. (I'm sure one could do experiments though, in which a very controlled light source could be used, demonstrating the relevance of the angle of incidence of the light.)

A coin whose toning is more irregular in profile ("mountain range") would have similarly wild toning, like this example:

A coin with a uniform toning layer, whose color is based on the thickness of that layer, does not take on additional colors by rotating in the light. Here is an example showing only slight gradation towards the perimeter:

If I tilt this coin in the light, I cannot get the colors to change to blue etc. Again, the reasons for this are complex, as one might reasonably expect the changing angles to affect the extra distance travelled by ray C, and therefore the perceived color of the exit light. Part of the explanation may be that the color is caused not only by the thin film interference, but also by selective absorption in the toning layer itself. This would imply, for example, that if the toning layer comprised different molecules, the colors would be affected. For example, a sulfur-rich toning layer would appear different from an oxygen-rich toning layer of the same thickness. And this is in fact true; silver sulfide yields more colorful toning than a film of oxides. But mostly it is about the thickness of the toning layer and the interference phenomenon: the film layer is too thin to get much red-green cancellation, no matter what angle the light comes in at.

Incidentally, the coins closer to the center of a stored Mint bag stayed asbolutely pristine and untoned, as any reactive gases such as oxygen or sulfur were absorbed by the outer coins in the bag, which therefore acted as a "getter." This is why so many thousands of "brilliant" or "white" coins came out of Mint bags. This in turn fueled an appetite to collect Morgans that are untoned, "blast white," as that is what was primarily available. However, once out of the bags, these coins would begin to tone over time. To feed the marketplace for white coins, it became common practice to dip Morgans en masse. Even Mint bags containing beautiful rainbow-toned coins were sometimes dumped wholesale into bathtubs filled with dipping solutions. In today's market, the preference for white Morgans still remains, although I am doing my best to increase awareness and appreciation of naturally and beautifully toned Morgans, which are more in line with our collective preferences for older classic silver type coins.

The mathematical model in the spreadsheet shown above begins to explain how such colors are in fact naturally possible. That's the amazing fact of these coins, that nature created this intense and amazing palette, with little help from us. Artificial toning would imply the use of heat or chemistry to accelerate or otherwise alter the reactive process, but coins like these Morgans cannot quite be reproduced in even the most clever coin doctor's lab. Look at hundreds or thousands of toned Morgans, and you will gain an appreciation of what is possible by natural processes.

<<If I get this (even a little), are you saying that a coin with multiple colors has a toning layer of varying thickness, and it is the change in the extra distance traveled by the reflected light penetrating the film which phase shifts and ultimately causes the colorful look?

Is this also why, as we tilt a coin in hand, we see new (or maybe enhanced) colors and a change in luminosity?

Or maybe it's the phase shifting of many rays of light because some only partly penetrate the toning layer before reflecting? Does that happen?

Or maybe it's due to that intermediate phase shifting thing.

Or maybe I don't get this even a little.>>

YES to to the first question; it is variations in the thickness of the (extremely thin) toning layer, and the change in the extra distance traveled (and therefore the degree of phase-shifting) that causes the interference phenomenon.

YES to the second question, but the "cartwheel" effect is also due to what we call Mint luster, a quality of the surface finish on pristine coins that results from the metal flow during striking.

Probably NO to light penetrating the toning layer to a partial depth, and reflecting back before it reaches the coin's surface.

<<Toning occurs on a silver surface due to the accumulation of a film( various sources) which are seen as different colors, due to the thickness of the film.

The colors progress, with the addition of more film.

Right?>>

Yes, that's basically right. Once the film gets too thick, the toning will simply appear dark or black, as it also absorbs more light, so the total luminosity of the reflected light declines, and there's not enough at any wavelength to trigger our perception of color.

<<Is the toning the affect of certain chemicals from the environment interacting with the copper in the silver. Producing a film that's part metal and part chemical? >>

It is true that the toning is affected by (in fact caused by) its environment. And it is true that some environments will not produce all the colors. But it is not true that this happens "no matter how thick or thin the toning develops." If you can get a thin film of toning to develop, in the range of 100 to 600 nanometers' thickness, then you will see the corresponding colors produced by this phenomenon. The cases where it doesn't happen are the cases where you don't get that thin film; either

a) The toning conditions are so non-reactive that you don't get a toning layer at all; or

b) The toning conditions are so reactive that the thickness of the toning rapidly blows past the upper end of the range where this effect occurs, so the toning just progresses to dark and unattractive.

Also, if the coin's underlying surfaces are not reflective, so the luminosity of the total reflected light is too low. This is why you won't typically see banded rainbow toning on circulated coins, although if the toning environment is sulfurous enough, you will still get colorful toning, such as on the circulated early silver type coins from the Queller collection. Circulated coins, unless dipped, also may have a protective layer of oils on the surface that prevent the formation of oxides and sulfides, giving a dulled and colorless appearance.

Once you get well beyond the "thin film" range, then the inherent optical properties of the toning layer itself become relevant. Every chemical compound has a "color" caused by the way it absorbs and reflects light. So in this respect, what leo is saying has some truth to it, for thicker toning layers. For example, we all know that heavy copper oxides can appear green or cyan. This has nothing to do with thin film interference, but rather with the fact that this particular compound absorbs red light, thus allowing blue+green=cyan light to reflect. A suitably thin film of copper oxide, however, can still produce all the colors of the thin film interference progression.

<<Your explanation makes sense in the case of coherent light, however we are not viewing the coins under laser light. Natural light has no coherence, therefore the incident rays are of all phases. So how is it that cancellation can occur when incident and reflected rays have a random phase relationship?>>

that's part of the nature of light, that it can behave statistically like a wave function despite also comprising individual photons. For example, the two-slit experiment provides a wave-like interference effect without having to use coherent laser light. So the light behaves as a statistical aggregate of individual waves. Another way to look at it is that each incident ray is divided, with a portion bouncing off the upper surface, and the balance traveling the extra distance. In that case, the interference will occur. You will say, "but that's impossible, you can't divide the individual waves." Yet light does behave that way; on the quantum level, the behavior somehow adjusts to produce these wave-like effects on a macro basis. The wave-particle duality is one of the great mysteries of quantum mechanics - I have my own theories, but not for this forum !!

It's not a great explanation, but the best I can offer without brushing away more cerebral cobwebs.

<<I have always wanted to do a controlled experiment to determine if increasing toning on a silver coin adds weight to the silver coin or not.

Have you or anyone else ever attempted to explore or test this?>>

In theory the toning adds to the mass of the coin, because it represents reaction of the metal surface with ambient gases. So when a silver sulfide or copper oxide molecule is formed, the atom of silver or copper remains on the coin, but is now joined by sulfur or oxygen from the atmosphere. Therefore the mass of the additional sulfur or oxygen increases the mass (and therefore weight) of the coin. However, the increases are vanishingly small for thin toning layers, and could not be measured with ordinary equipment.

<<Question: Is the color progression different for other base metals?

Discussion: Although my sense is they follow the same general progression, it seems to me that Nickel and Copper tone a bit differently than silver -- for instance yellows and blues are much more prevalent on nickel than silver or copper -- yet this seems at odds with my understanding of thin film interference.

Does the different underlying color of the natural metal come in to play here? Is it some other feature of the metals (perhaps the nature of their oxides and sulfides)? Or is there something else I'm missing?>>

Other metals will exhibit differences in the color progression. Copper will be noticeably different due to its own color. Our perception of color does not reflect something inherent in a substance, but rather its ability to absorb light at various frequencies. Even paint pigments appear the way they do for this reason. In other words, yellow paint is not inherently yellow; rather it is its ability to absorb blue light that makes it appear yellow when illuminated by full-spectrum white light. Copper appears red-orange because of its ability to absorb some blue and green light. Therefore, the reflected light from a copper surface will not have all the same wavelengths present as light reflected of a bright silver surface. This in turn affects the interference progression. There will still be a thin film phenomenon, and a color progression, but somewhat modified from the one for silver coins.

On nickel I would expect the progression to be closer to that of silver, but I have not studied enough toned nickel to verify this.

My observation & toning classification system were intended only for use on silver coins, at least for now.

<<I have a problem/question with all of this. For this to be true, one must assume that a coin's surface is quite smooth. However, my understanding is that a freshly minted coin's surface has many minute ridges from the stretching of metal when the coin is struck. These micro-ridges produce the shimmer we call luster. When one dips a coin, these ridges are reduced and obliterated to form a more smooth surface. The same thing happens from handling, causing a coin to lose it's luster with increased handling. Coins which have been polished or dipped often develop colorful toning because of the artificially flattened contour of the coin's surface. Likewise, proof coins often show more rapid and pronounced toning than MS coins.

Assuming the above to be true, the undulating surface of an uncirculated MS coin with a uniform layer of oxide should refract a variety of colors because the angle of incidence of light is changing over the micro-contour or microscopic surface relief of the coin. Therefore, one should see a mix of colors (with a prevailing color reflecting/refracting directly back at the viewer), and a variety of color transitions with increased depth of the oxidized layer and the surface topography of the coin. A small point on the coin should change color as the coin or light is moved.

I say this because I'm trying to make sense out of a very dark coin I have (Lincoln commemorative half) that shows rich color when I tilt it to directly reflect light into my eye. The colors are a deep coppery russet toning with dark blues, sky blue, yellow, orange, and magenta under intense light and magnification (7-45X). This color gives way to glossy black around the lettering. Held in hand under normal lighting and the coin looks dark brown to coppery colored unless tilted properly into bright light. >>

Excellent questions and observations. There actually is a scientific answer to the points you raise, although it took me a while to figure it out. First, notice in this diagram that the angle of incidence of ray C is much closer to 90° than the angle of incidence of Ray B:

The reason the angle of incidence changes is the difference in the index of refraction between air and the toning layer. The much denser toning layer permits transmission of light, but causes the ray to bend when it enters. As a result, the angles of incidence of all rays that penetrate the toning layer fall into a narrower range of angles, closer to 90°. Therefore the extra distance traveled d=2t/sin(x) stays relatively close to 2t, as the value of sin(x) is relatively close to 1 for values near 90°. This means that for light penetrating the toning layer, tilting the angle matters less than you would think. Also remember that while there may be a bunch of rays with different trajectories, your eye perceives only the statistical aggregate of them, the peak of the bell curve distribution.

As to coins that have a layer of "old time" brownish toning, that suddenly come to life with reflected colors at just the correct angle, I think there is an explanation for that also. I suspect that for some toning layers, the surface density and refractive index of the toning makes it difficult for much light to penetrate, unless the angle of incidence is close to 90°, or at least greater than some threshold angle x. So if you tilt the coin too far, then the incident rays come in too far away from a perpendicular angle to the surface, so most of the light gets absorbed by the toning layer, or reflected off the upper surface (ray B) and does not penetrate and reflect (thus no ray C). The result is that you only see the brownish black color of the toning layer. However, when you tilt the coin just right, the angle of incidence gets above the threshold angle, closer to 90°, and then the light can penetrate and reflect (ray C), and you see the underlying colors produced by the thin film effect.

Article by: Doug Kurz (dkurz@mindspring.com)
Compiled and by Brandon Kelley (brandon@jhonecash.com)
Edited and reprinted here from Doug Kurz's Article on the PCGS message boards with the permission of Doug Kurz.